Article 2: A More Sophisticated Approach
In an article posted prior to this one, I presented the basics for making simple aluminum disk gongs. This follow-up article assumes that you’re familiar with the approach described there, so if you haven’t read that article already, have a look at it before reading this one. That article discussed things like materials and where to obtain them, and described the simple method for hammering the nipple in the center, by which the gong is to be tuned. This article picks up from there, describing an approach to tuning that is more sophisticated than the rudimentary approach described in the first article. This article also touches on the underlying acoustics more than the previous one. For photos and audio of the gong set in keeping with the ideas set out in this article, see here.
To reiterate an important Important disclaimer pertaining to both articles: These notes are not about the making of traditional Asian gongs. That time-honored discipline is well beyond the reach of this writing. Rather, these notes concern the making of simple disk gongs with minimal hammering and no hot forging required.
One of the key points of discussion in this second article is the musical relationships between the overtones within the gong tone, and I’ll start with an overview of this topic.
Gong sounds, like the sounds of most musical instruments, contain not just a single frequency, but many frequencies sounding simultaneously. In their blend, these frequencies help create the characteristic tone quality of the gong.
With most musical instruments, our ears effortlessly recognize one of the many frequencies present as the fundamental. We hear that frequency as the defining one which gives the tone its recognizable pitch. Normally this is the lowest of the frequencies present. Other frequencies above this are thought of as overtones. They contribute to the overall tone quality but are less essential to the sense of pitch.
For many instruments, such as most string and wind instruments, the overtones are harmonic. This means that the overtone frequencies appear in a series reflecting a simple mathematical relationship between the frequencies. The timbre of sounds with harmonic overtones typically seem coherent and integrated, and they have well defined pitch. Gongs, however, are different in this regard. Not only are the many pitches present in the gong tone not harmonic in their relationships, but even the idea of a single linear series of frequencies, with fundamental as the lowest and overtones arrayed in a single orderly sequence above, is a bit shaky. (This is a characteristic that gongs share with drums and bells.)
To get a picture of how this works, we need to look at the physical basis of the frequencies that are sounding. In gongs, as in strings, winds, and other instruments, each of the frequencies within the composite tone arises from one or another pattern of vibration which the physical sounding body engages in, commonly called a mode of vibration. If you’ll excuse a momentary digression (one that I hope will be an instructive), I’ll discuss the examples of strings and some other instruments before returning to gongs. With strings there is a certain recognizable pattern of oscillatory movement that can be referred to as the first mode of vibration. This is the motion that produces the frequency that we hear as the fundamental and that gives the string its recognizable pitch. Simultaneously, as part of the overall string motion, there is a second mode, a third mode, and so forth, each producing its own frequency. In strings, this series of frequencies happens to fit the mathematical definition of a harmonic series. In this case the overtones, with their harmonic relationship to the fundamental, tend to blend very closely with the fundamental in our perception; the ear scarcely recognizes them as separate tones. And, lining up mathematically with the fundamental as they do, they tend to reinforce the pitch-sense of the fundamental in our ears, creating a coherent and clearly pitched composite tone.
In some other vibrating bodies, such as marimba bars and kalimba tines, a similar series of tones is in play. Once again the lowest frequency present is usually heard as the fundamental, and there is a series of overtones arrayed above. But in these instruments, the overtones typically are not harmonics of the fundamental; they appear at inharmonic frequencies. In such instruments we still usually hear the lowest tone as the fundamental providing a sense of recognizable pitch, but the effect is different from that of harmonic tone qualities. The inharmonic overtones may stand out rather than blending in, and the pitch-sense of the tone may be less clear. Sometimes, in such instruments, the bars or tines are reshaped to bring one or more of the more prominent overtones into a harmonic relationship with the fundamental. This helps clarify the pitch sense, and creates the impression of a more integrated tone quality.
And now back to gongs. Gongs are more complex in that there’s not a single linear series of overtones. With their large two-dimensional surfaces, gongs are capable of many different modes organized along two main types of vibratory patterns. One type of pattern is characterized by circular nodal rings, with movement in which adjacent ring-shaped concentric regions flex in opposite directions. The other involves nodes along diameter lines, with side-by-side areas moving in opposite directions. (These things are difficult to describe in words; have a look at the diagram for a clearer picture. 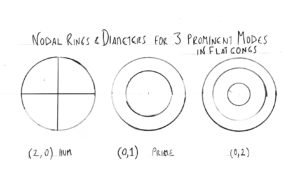 These diagrams are based upon illustrations in Thomas Rossing’s Science of Percussion Instruments, and the thinking underlying this essay owes much to Rossing’s discussion of vibrating disks on pages 79-80.) Some gong modes are characterized by one or the other type of motion; other modes involve both. The upshot is that many different modes of vibration are available in a single gong, and when you strike a gong, many modes are excited, producing a blend of many pitches. The frequencies of these modes don’t follow any familiar or musically meaningful pattern; they’re pretty much all over the place. Which of the many available modes are most prominent in the resulting tone depends on several factors including striking location, hardness of the beater and the size of the beater surface making contact.
These diagrams are based upon illustrations in Thomas Rossing’s Science of Percussion Instruments, and the thinking underlying this essay owes much to Rossing’s discussion of vibrating disks on pages 79-80.) Some gong modes are characterized by one or the other type of motion; other modes involve both. The upshot is that many different modes of vibration are available in a single gong, and when you strike a gong, many modes are excited, producing a blend of many pitches. The frequencies of these modes don’t follow any familiar or musically meaningful pattern; they’re pretty much all over the place. Which of the many available modes are most prominent in the resulting tone depends on several factors including striking location, hardness of the beater and the size of the beater surface making contact.
So how does the ear make sense of the gong tone? Does it recognize one of the many frequencies present as the defining tone, giving the sound a recognizable sense of pitch? Does it hear it as a sonic wash without meaningful pitch? Does it hear a chordal blend of pitches, some of them recognizable but none serving as a defining pitch? The answer is that any of these responses may arise with different gong sounds. As one example, in many of the beautiful large Asian gongs you’ve probably heard, there’s a rich sense of tonality, but in the lush complexity of frequencies present, the pitch sense may be ambiguous.
And this brings us back to the simple disk gongs that are the subject of this writing. They differ from very large gongs in that with these the tone is not quite so complex, making it easier for the ear distinguish particular frequencies within the tone. Let’s start by talking about the simplest possible gong: a flat circular disk with no boss or nipple at the center and no curvature to the surface. To be more specific, in keeping with the suggestions in the previous article, we’ll take as our model a disk of aluminum, between 3/32” and 5/32” thick, and between about 6” and 20” in diameter.
If you strike a disk gong within this size range somewhere off-center with a hard mallet, you’ll get a clangy tone with a mess of different frequencies. None of the modes will be clearly dominant, and as a result you’d be hard put to identify a single defining pitch in the resulting sound. On the other hand, if you strike in the center with a fairly heavy, soft mallet, the picture clarifies considerably. There is one frequency that stands out strongly enough that most people would not have difficulty hearing that tone as the defining pitch. In other words, even though there are many frequencies present, the gong produces what the ear can interpret as a recognizable note. My experiments suggest that this note corresponds to the mode of vibration which has no diameter line nodes, and one concentric nodal ring – that is, the mode identified as {0,1} in the diagram above. Center-striking brings it out strongly, because this mode’s pattern of vibration is most active at the center point.
In the sounds of most other musical instruments, the pitch-defining mode, called the fundamental, has the lowest frequency of all the modes present. With these gongs, however, this pitch-defining {0,1} mode is not the lowest frequency present. That honor goes to the mode identified in the diagram as {2,0}, with two diameter lines node and no nodal rings. In a perfectly flat and uniform gong, this tone typically sounds at a musical interval a little more than a major 6th below the {0,1} tone. But this lower mode is much quieter. Indeed, when the gong is center-struck, it is barely audible. This is partly because for {2,0} the center point is at the intersection of the two nodal diameter lines, meaning that this mode is not active at the center and the center-strike thus scarcely excites it at all. In practice, a center-strike or near-center strike actually will usually activate this low mode to some degree, but not enough to carry the day in the ear’s unconscious analysis: the much louder {0,1} mode dominates the tone enough to establish itself as the defining pitch. Borrowing from terminology used for carillon bells, I’ll refer to the dominant mode {0,1} as the prime tone, and I will refer to the quieter, lower mode {1,0} as the hum tone.
With careful listening it becomes possible to identify several more frequencies in the flat gong sound, all of them higher than the prime tone. Depending on your choice of beater and on how perfectly centered your center-strike is, different ones among these will stand out more or less. But if you’ve developed your ear to where you can distinguish the more prominent frequencies in a complex tone such as this, a couple of them can be heard standing out fairly strongly. In a perfectly flat gong, one of them appears just over a major ninth above the prime. Analysis shows that this tone is associated with the mode {1,1} with one diameter-line node and one concentric nodal ring. Another can be heard about two octaves and a minor second above the prime. This is the mode {0, 2}, with no diameter line nodes and two concentric nodal rings.
As discussed in the previous article, the flat gong can be tuned by hammering a small rise in the center, called the nipple or the boss. Doing this has the effect of stiffening the disk, causing the pitch to rise. In an ideal situation, the prime tone of the flat disk is below the pitch you intend to tune the gong to, and you can bring it up to its intended pitch by hammering, being careful not to hammer too much and push it sharp.
At this point you might ask the question, will hammering the center raise all the modes simultaneously, and by the same amount? The answer is that it will tend to raise all modes, but not by the same amount. And this suggests an interesting possibility. In the flat gong, the various audible modes produce a set of seemingly random, musically unrelated pitches. If the different modes can be affected differently by reshaping the gong, would it be possible to reshape in such a way that the several audible modes realigned themselves in a more coherent set of pitch relationships?
To clarify this idea and provide background information, let me make another digression. As discussed above, in most of the most familiar musical instruments, including most winds and strings, the overtones are aligned harmonically over the fundamental. With this relationship in place the overtones blend closely with the fundamental to produce a tone of clearly recognizable pitch. In other instruments, such as marimbas and kalimbas, although there may be a clear fundamental with overtones arrayed above it, the frequency relationships are not harmonic. Listeners can usually still clearly recognize the fundamental and identify the pitch, but the tone quality is more complex and the pitch sense is not as clear; in some contexts there may even be musical confusion created by the prominent and harmonically unrelated overtone pitches present in the tone. Some makers of these instruments – most notably marimba makers – carefully reshape the bars to alter the patterns of movement for certain modes of vibration in a way that shifts the frequency relationships of the fundamental and the most prominent overtones. The intent is to place the overtones frequencies in harmonic relationships with the fundamental. This has the effect of clarifying the tone and making the pitch sense clearer. Some might say this makes the tone less colorful and more boring, but there can be no doubt that it has the effect of reducing ambiguity and making the tone seem more “in the pocket.” The most obvious frequency relationships to strive for in doing this would position one or more of the overtones in octave relationships to the fundamental. If one or two of the overtones stand at one or two or three octaves above the fundamental, that goes a very long way toward clarifying the tone and disambiguating the pitch sense. That done, there will still be other modes producing overtones at various inharmonic pitches. These may add spice and color, but with those octaves in place the pitch sense still locks in clearly.
The techniques for reshaping bars or tines to align the overtones are known and understood, and not dauntingly difficult to apply. But how might this apply to gongs? It turns out that, as a practical matter, it is a lot easier to apply these reshaping rules to linear sounding bodies like bars and tines than it is to two dimensional shapes like flat gongs. In theory it could be done; in fact it could be a very enjoyable project for someone who is both mathematically inclined and skilled in computer-aided manufacturing techniques. But for someone operating in a home workshop, it would be quite a challenge. For myself, I haven’t so far come up with a viable approach.
… But wait! In an unlikely bit of luck, it turns out that in hammering the small nipple at the center of a flat going, it can fortuitously happen that three of the prominent flat gong modes described above come reasonably close to octave alignment. As shown in the diagram, the alignment is between the prime mode {0,1}, mode {1,1} at an octave above the prime, and mode {0,2} at two octaves above the prime. The result is the creation of a gong tone that is more coherent and clear in pitch than a flat gong with the usual inharmonic relationships in the dominant overtones. Yet plenty of inharmonics remain present in other modes, creating a tone that is clear and full, yet still distinctive, interesting, and complex. I happen to love this tone, and that’s why I’m writing this article with a lot of enthusiasm. Notice that this situation is not so much a matter of deliberate analysis leading to controlled overtone tuning; it is mostly just a matter of luck and happenstance in the way the physics of flat gong modes works out. That said, there is room for skill on the part of the gong maker here, because getting the three tones into alignment is a matter of hammering the nipple just right. Make the nipple a little different – a little too big or too small, or a little too narrow or a little too spread out — and you’ll miss the alignment.
So, starting with a flat gong of reasonable diameter and thickness, it should be possible to create a finished gong with suitably sized nipple in which the overtones thus align, at least approximately. But now we need to ask, at what pitch? If you want to tune your gong to any particular pitch, or if you want to make a tuned set, you will need for two things to line up correctly: The point at which you’ve done just enough hammering of the nipple to bring the overtones into alignment must also happen to be the point at which the gong has arrived at its target pitch. Is there a way to plan for that?
To answer this question, we can start by asking, “In the process of raising the original pitch of the flat gong by hammering, how much does the pitch of the prime tone need to go up before the overtones come into octave alignment?” If the answer to that is a consistent value, then it should be possible to start with a flat gong whose prime is that much lower than the target pitch, and hammer it up to pitch knowing that, if all goes well, the octaves will align when the target pitch is achieved.
In my experience, the needed pitch-rise is about 220 cents. (A cent is one one-hundredth of a semitone. 220 cents is two semitones plus 20/100 of a semitone. Most electronic tuners are calibrated in cents.) Thus, if you start with flat gong whose prime is 220 cents below the target pitch, and you hammer the nipple just right, then with luck you’ll come reasonably close to octave alignment between the three prominent modes at the point where the prime reaches the intended pitch.
But it may be simpler to think in terms of frequencies than cents, so here’s the equivalent information stated that way: the interval of 220 cents corresponds to a frequency ratio which, written as a decimal, comes out to .880. Thus, you want the frequency of the prime prior to hammering the nipple to be .880 of the frequency of the intended pitch. We can also translate this into diameters: for two gongs of the same thickness and material, for gong A to be 220 cents higher than gong B, the diameter of gong A should be .938 that of gong B; or (same thing) the diameter of gong B should be 1.066 that of gong A.
From here on out, this article gets more technical and possibly boring. Feel free to bail. To start, let’s get more explicit about the underlying rules of flat gong tuning:
Frequency is inversely proportional to the square of the diameter
Frequency is directly proportional to thickness
To put this information to use, you need to somehow determine the diameter for a flat gong tuned 220 cents below your target pitch – or, stated the other way, whose frequency is .880 of the target frequency. There are various ways to do this. Here’s one: Start with a sample gong of any diameter within the general range of diameters you expect to be working with. Make note of the frequency and pitch of the gong’s prime note. Hammer the nipple at the center of the gong to raise that to the point where the overtones align reasonably well. (This hammering/tuning procedure will be discussed in shortly.) If what I’ve said here is true, the desired alignment will happen when the gong is about 220 cents above its original pitch. Make note of the new pitch and frequency. Now you can (assuming some math chops) calculate diameters to yield desired frequencies in other gongs of the same thickness and material based upon this sample gong. The formula is: where f(sample) is the frequency of the sample gong, f(new) is desired frequency for the new gong to be made, d(sample) is the diameter of the sample gong, and d(new) is the suggested diameter for the new gong to be made, the formula is:
d(new) = [square root of f(sample)/ f(new)] times d(sample).
In theory, the flat gong you get by this calculation should be the famous 220 cents below the intended pitch, and will arrive at the intended pitch when you tune it up.
If you’re tuning to pitches within the standard 12-equal tuning system, then once you’ve got one gong tuned to a pitch within that system, you can use standard factors to determine diameters for gongs to be tuned to other pitches within the system. I won’t give the full list here, but here’s a start: to make a gong a semitone higher than a known gong, make the diameter 0.9715 as large. For a semitone lower, make it 1.0293. These semitone-up and semitone-down factors can be applied repeatedly to determine other intervals within the 12-equal system.
All this assumes that you’ll be able to cut gong disks to very precise diameters. This is a challenge in a home workshop, but not impossible. For my own gong set, I arranged to have the disks cut on a laser cutter. My specs were input and the cutting done by Ian Saxton, with flawless results. Thanks, Ian.
This also assumes you’ve got a good tuner on hand. The simplest approach these days is to use one of the smart phone or computer tuning apps: you play the tone; the app tells you the frequency and the pitch with cents deviation from the nearest 12-equal A-440 pitch. I often use an app called Plusadd Tuner; it’s just of many available. Note that this type of tuner app will decide for itself which of the many frequencies present to regard as the prime or fundamental, indicting the frequency for that tone. If you strike the gong at the center with the right sort of beater, they app will usually hear your prime correctly. (For a more sophisticated picture, try using a spectrum analysis app — there are many of these available too — which will create a graph showing all of the frequencies present, allowing you to zero in on whichever of them you’re interested in to get its frequency.)
Here are a couple of important caveats. I have found the inverse-squared relationship for diameter to be admirably accurate for flat gongs as long as the material is consistent and the thickness tolerance is very tight. But if there has been any bending of the supposedly flat gong, even seemingly minuscule and scarcely observable, all bets are off. As for the direct proportion rule for thickness: I have found this to be much less dependable. For that reason, I recommend that you work from a sample gong for each thickness you intend to use, making calculations from there based on diameter, and avoid using the thickness rule to calculate expected frequencies from one thickness to another.
You could ask: are there ways to calculate flat gong frequencies from scratch without having to work from samples? The answer is yes, but to do so you need to know the properties of the material you’ll be working with. The math is much more complex and in any case these properties may vary for materials from different sources, and it’s probably both simpler and more dependable to work empirically from the samples.
And now, more details about the actual gong cutting and hammering processes.
As discussed in the earlier article, you can sometimes find aluminum disks ready cut at metal scrap yards. If you aren’t tuning to a particular scale, you can make very nice gongs at low cost from this material. For tuning to particular pitches and scales, however, you’ll need disks of certain precise sizes, and so will have to cut them yourself from larger sheets or have them cut for you.
The hammering process is described in the previous article. Please refer back to that for the basic step-by-step. But where that article speaks of tuning the prime tone only, we’re now going to talk about tuning two or three modes.
To start with, you’ll be listening for the pitch of the prime mode {0,1}. To bring out this mode when you check for pitch, strike at the center with a fairly large, soft, heavy beater such as a large superball on the end of a stick. If you use an electronic tuner, the tuner will probably be able to read this mode without too much difficulty. You can also tune this mode by ear by comparing the gong pitch to the desired pitch sounded on an electronic keyboard or some other tone source.
As you continue the process, you’ll also be listening for the two overtones. For these it will be more difficult to recognize and identify the pitch. Under normal circumstances the tuner won’t be able to recognize these pitches, and without a lot of practice most people find it very difficult to hear and them clearly with the naked ear. (This is where spectrum-analysis software may be useful, if you want to get into it on that level.) To help with this, here are some tricks for bringing out the sound of these modes more prominently. With these methods the overtone pitches will be easier to hear by ear, and you may even be able to isolate them enough to allow the tuner to pick up on them.
For the prime mode {0,1}, as mentioned above, you can do quite well by center-striking with the heavy, soft beater. Suspending from points somewhere in the nodal ring at about 1/3 of the disk’s radius from the outer edge, as recommended above, also helps bring out this mode.
For the mode {1,1} which we’re hoping to align at an octave above, strike not at the center, but in that 1/3 r ring, using a slightly smaller, harder mallet (but not overly hard, which will produce too much clang sound). This trick of striking in the nodal area of the prime will tend to excite the prime less, making it easier to hear the {1,1} mode instead. You can further improve the result by resting a finger gently at the center of the gong while striking, which will also tend to damp the prime along with other modes that are active at the center.
To bring out the {0,2} mode that we’re hoping to align at two octaves above, strike the gong gently but very accurately at the center with a small, hard beater such as the end of a ¼” steel rod. This may be good enough to let you hear {0,2} clearly, but you can also try a gentle finger at a point a little more than half the radius in from the edge. This may help to quiet the prime, allowing you to hear {0,2} a bit better.
The idea is that as you bring the prime up to its intended pitch, the other overtones will align at something close to the hoped-for octave relationship as well. I confess that I’m still depending a bit on luck to get those overtones to align, and I’m not always successful. But my luck has been a little better when I make the nipple fairly narrow. This can be done by hammering it into a relatively small hole in the board you use for backing when hammering – close to one inch for smaller gongs; a little bigger for larger gongs.
In this article I’ve been talking about a particular set of overtone relationships involving octave alignments. This is by no means the only possible set of relationships to strive for or to enjoy in the gong sound. Approaching the hammering a little differently will yield different relationships. For instance, hammering over a much larger hole will result in a larger nipple and a generally more curved gong surface, resulting in other overtone configurations. Similarly, doing more hammering to raise the prime more than I’ve suggested will likewise alter the outcome. These things can be fun to explore. Effective tunings can be found in which a prominent overtone is tuned an octave and a fifth, or perhaps two octaves and a fifth, above the prime.
And please remember that you are in no way required to pursue the idea of overtone tuning if you don’t want to. You may prefer to ignore the overtone question entirely! If you do that (as described in the first of this pair of articles), you’ll get gong tones with whatever relationships between the different modes you happen to end up with. The results may sometimes seem odd or exotic, but more often than not the resulting gong sound will be pleasing to the ear.
