What happens when two or more musical strings are connected to one another? There are many ways that this idea can play out, and in this article we’ll look at some of the possibilities. The musical results can sometimes be quite interesting! You can see a version of this idea in action in this recently posted video. I first explored the idea of conjoined musical string systems long ago, and we ran a series of articles on the subject in the late great Experimental Musical Instruments journal in 1991 (see the articles here, here, and here). More recently I’ve made a YouTube video where you can see and hear a conjoined string instrument in action. It may be a little hard to picture some of the possible configurations for conjoined string systems, so let’s start with descriptions.
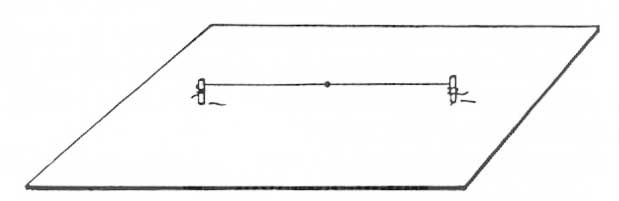
Two strings joined end to end. When they’re tightened, they align to form something like a single string (but probably with some uneven weight distribution).
If you simply attach two strings end to end and tauten them between two end points, they’ll just pull into a straight line like a normal string. There might be a lump of extra weight in the middle where they join, as you can see in the diagram, or perhaps the two halves will have different thicknesses. This uneven weight distribution can be interesting from both an acoustic and a musical point of view, because it alters the compound string’s overtone recipe, but this sort of linear system is not the focus of this article. (You can learn more about weighted strings in this video, and see more descriptions here.)
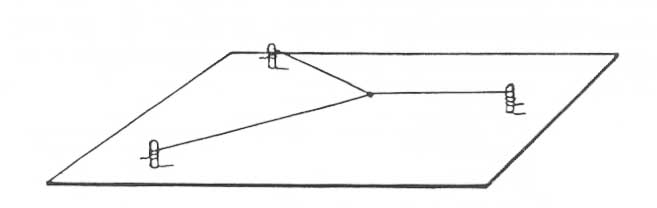
A three-string cluster. This form can be made from three separate string segments joined at the center, or from two segments with one attached to the midpoint of the other and tightened.
So let’s look at the next possibility. What if, starting with two strings, you attach the end of one to the midpoint of the other, and tighten both? In this case, the tugging by one string at the midpoint of the other pulls what would originally have been a linear string into the two legs of an angle, with the attached string forming a third leg. This adds up to something like three spokes of a wheel (but with no wheel), as shown in the diagram. It becomes, functionally, a three-string cluster, similar to what you’d get if you started with three separate strings and joined them at a center point. Depending on how you tension the strings, they can be all the same length, with the joining point at the center, or they can be different lengths with the joint off-center.
In an addendum to this article I’ll discuss the acoustics of this sort of three-string configuration in more detail. For now though, let’s look at the big picture. The first thing to notice is that these three-string systems produce many tones simultaneously – not just a fundamental and its harmonic series (as with conventional strings), but several such series which are not constrained to be harmonic relative to one another, plus several additional modes which likewise may or may not be harmonic. (I’m using the word “harmonic” here in its mathematical and acoustic sense, not it’s musical sense.) These are frequencies associated with individual string segments operating independently, as well as frequencies involving segments in interaction, plus the whole system vibrating as one. It adds up to a complex, quasi-chordal string timbre; typically a bit outside of the familiar tonal box in its frequency relationships. These relationships are not fixed; they’re variable according to how you handle the string gauges and subsequently tension them. By adjusting these things you can, in effect, tune the timbre. Within that resulting timbre you can also vary the tone by your choice of plucking location and direction of pluck, highlighting different frequency blends within the overall mix.
Tuning the timbre! It’s a most inviting idea. So I should clarify right away that the process is not a very controllable one. It’s hard to prescriptively create designer timbres here. The reason is, every little thing you do in selecting string gauges or adjusting the relative tensions affects the whole system, altering not just one frequency in the mix but the whole gamut. It’s difficult to manage with precision.
In my own multi-string explorations, I don’t try to operate prescriptively. Given a three-string system I want to tune, my typical approach is to mess around with the string tensions until I find a sound that I like and that seems musically promising. If there are multiple three-string clusters present (as there are on some instruments that I have made), then there’s lots of back-and forth between different clusters as I seek out relationships that work well together. Tuning to standard scales is difficult, but exploring in search of intriguing non-standard tonal territories can be rewarding.
And now let us add another layer of complexity into the mix. You can play a three-string cluster by plucking with the strings “open,” as we’ve been discussing, or you can modulate the pitches with a slide. Place the slide somewhere on any of the segments, and the vibrating length of that segment is shortened, raising all frequencies associated with that segment. Depending on how and where you pluck, you may also hear a new frequency associated with the portion of the string on the other side of the slide. The whole-system frequencies will be changed as well. By pressing the slide with greater or lesser force, you can vary the tension on all segments, creating vibratos and pitch bends. Moving the slide along the string as it sounds also bends the pitch, not only of the individual segment but also of the whole-system modes. These frequencies don’t rise and fall in parallel; some move faster or slower than others — for instance, while the tone of the segment being slid upon might rise by, say, an octave, the whole-system tone might rise by something like a fourth. Sometimes you can hear tones both rising and falling simultaneously, as the sub-segments on opposite sides of the slide move contrarily. Using the slide in these ways you can do a peculiar sort of melodic-chordal playing, or you can pointillistically explore the variable tones and timbres.
It’s all very complex – so many timbal possibilities! And in fact, for my ear, it easily becomes too complex. With so many uncurated frequencies grinning at me, there’s the danger that the ear becomes tired and stops trying to hear it all. The perceived effect may reduce itself, subjectively, to a lot of undifferentiated inharmonic clanging and twanging. It can be worthwhile to seek ways to simplify, giving the ear a bit of a break and feeding it more organized melodic or harmonic information to respond to. One way to simplify is to tune two of the segments to the same tone, thus reducing the number of frequencies present. This has a secondary, very appealing effect: the like-tuned segments will tend to chorus together nicely. The effect is still richer with a bit of vibrato-y tension modulation on the third segment using the slide. Alternatively, you can use a fingertip on the third segment in place of the slide, damping the third segment and simplifying the tone of the remaining unison pair to something close to a single (but warmly chorused) string tone.
With the whole system sounding, the lowest tone is the whole-system fundamental. We know that in any tone quality the ear is inclined, when possible, to hear the lowest frequency present as a pitch-defining fundamental. With the three-string systems, it might be nice to try to configure things so that this lowest pitch relates in some meaningful way to the diversity of tones arrayed above it. If you equalize all the segments so that they produce the same pitch individually, then this whole-system fundamental tends to show up just a little more than an octave below the segment fundamentals above, frustratingly close to what would be a very coherent tone quality. Perhaps if it were possible to make the three-string configuration with zero additional weight at the joining point you’d get octave alignment, but as a practical matter that would be difficult to do. Oh well …
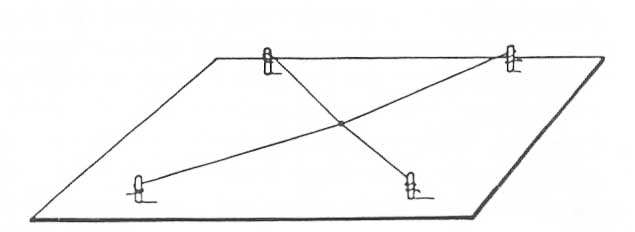
A four-string star configuration. This one can easily be created by crossing two strings.
I’ve been talking so far about one of the simplest conjoined-string configurations, three-string clusters joined at a middle point. Of course there are many more possible configurations. These include similarly center-joined star-like clusters but with more than three spokes. It also includes any number of other arrangements – think for instance of groups configured like a distorted H, or a crazy K. You can see one reason not to do this: more complex forms with tend to give rise to more complex timbres – which is to say, more unruly frequencies – which you may not want. You can see a few possibilities in the diagrams on the right.
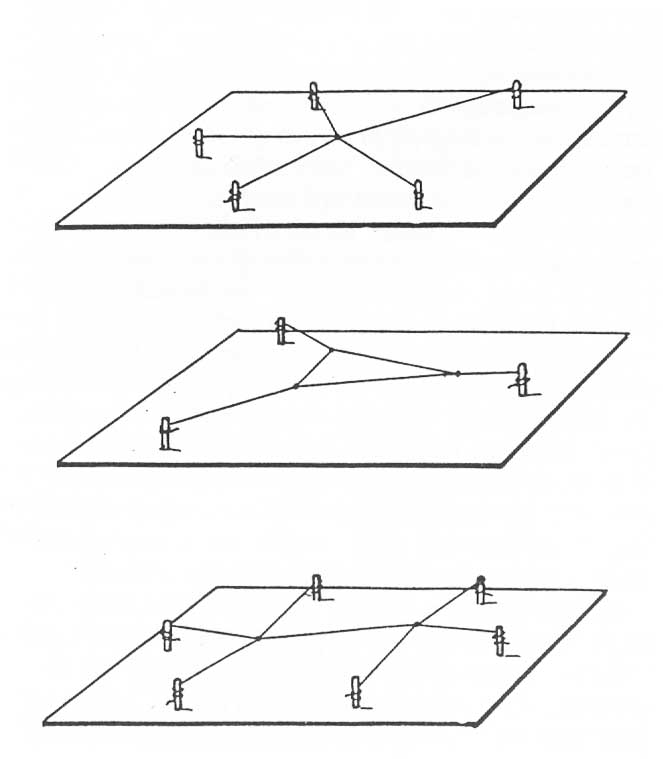
Many more two-dimensional multi-string configurations are possible; three examples are shown above. Admittedly, this is all just fun speculation; I’ve never actually made these configurations.
There’s one mitigating factor which has the potential to open up an interesting musical approach (but which I admit I haven’t explored much myself): with large, complex many-string systems – think of the H or K but with many more strings angling off one another in various ways – it might become possible to play in a more localized way within the system. That is, plucking here or there might activate different parts of the configuration much more than others, giving rise to a greater variety of tones and timbres depending on where you pluck. By the way, my talk here is nothing more than fun speculation; I’ve never actually made the more complicated multi-string systems shown in the diagrams on the right.
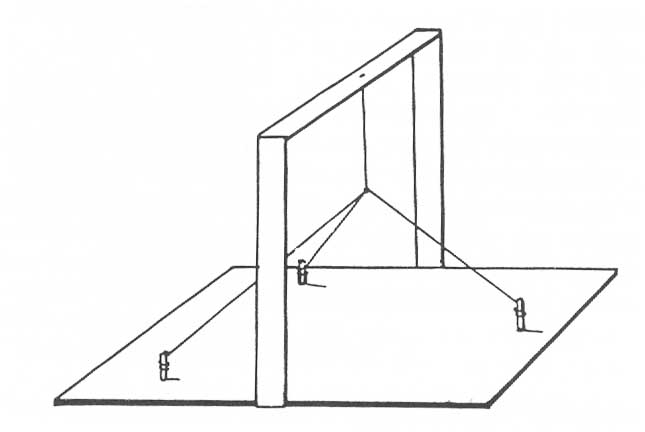
In this three-dimensional system, any would-be whole-system modes are immobilized by rigidifying effects.
If you work in increasingly complex configurations, be aware that if you include the third dimensions – that is, if the strings are not all in a single plane — you will actually reduce rather than increase the number of possible vibrating modes. 3-D configurations actually eliminate whole sets of modes by immobilizing them. To take the simplest example, in star-like systems the whole-system modes become impossible if the spokes are not flat in a plane, as the rigidifying effect of including the third dimension prevents the up-and-down movement that is essential to the whole-system modes (as shown in one of the diagrams on the right).
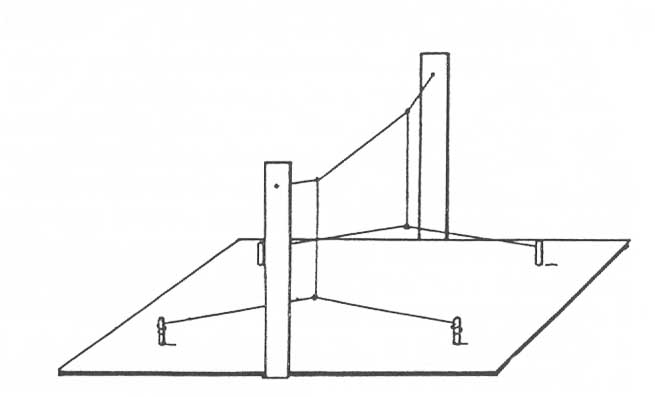
… but here is a 3-D system which does allow some interesting additional modes.
We can further expand the horizons if we consider other ways you can put multiple strings in interaction with each other. For instance, think of the prepared-guitar trick of running something like a knitting needle perpendicularly through the six strings, over-under-over-under-over-under. When you do this, the vibration of one string is strongly communicated to the others through the shared knitting needle, and all contribute to an appealing, tonally complex, bongy sort of timbre.
The knitting needle is just one such approach; there are many variations on the underlying idea of somehow putting multiple strings in communication with one another through a shared non-rigid anchor points or bridges of some sort. Some of these ideas are discussed more fully in the Experimental Musical Instruments articles referenced at the top of this article.
I’ve made several instruments with conjoined strings in one form or another. The one most closely reflecting the ideas discussed in this article is Trillium Cluster, featured in the video mentioned above.

Trillium Cluster, conjoined-strings instrument with eight three-string systems on a soundboard.
It’s a set of eight three-string clusters, large and small, arrayed on a 20″ x 26″ sound box. I tune it, as described earlier, by messing around until I find a set of tonal relationships that I like among the many clusters. I play the clusters both open and with a slide.
Addendum: More On Three-String Clusters
For those that may wish to nerd-out a bit more on the behavior of these systems, here are some notes on the acoustics. These notes are specifically about simple 3-string star-clusters and don’t address more complex systems, but with a bit of thought you can extrapolate some of the ideas discussed here.
Each leg of the three-string cluster can vibrate independently just as a normal musical string would, with a fundamental and harmonics determined by the length, mass and tension as expected. If all the strings are equal in l, m and t, then all will produce the same fundamental and overtone frequencies. If you use strings of different gauges, then the masses will differ and the segments will produce different frequencies. The length and tension factors are in interaction: tighten one string more than another and the point where the three strings join is pulled off center. Tension will tend to equalize but the lengths of the three segments will now differ, again resulting in different frequencies among the segments. Thus you can have three different string segments each producing different harmonic series.
In addition to the modes for the individual segments, there are whole-system modes in which all three strings move together. These modes differ from normal string modes in their patterns of movement. While a given point in a normal vibrating string can move through 360 degrees, up and down or sideways, the whole-system modes are constrained by the way the three strings tug at one another and can only move in the up-and-down direction. In this the system is analogous to a vibrating membrane, which likewise has only up-and-down motion. The most prominent of these whole-system modes, which could be called the whole-system fundamental, involves the mid-point vibrating up and down at a frequency typically much lower than any of the individual string segments. Other up-and-down whole system modes may occur which are analogous to higher membrane modes. We’d expect these to be inharmonic relative to the whole-system fundamental.
Beyond the individual string modes and the membrane modes still other modes are possible, some involving two of the three string segments. Depending on lengths these modes may or may not appear in harmonic relationships.
